안녕하세요!
오늘은 금융시장에서 활용되는 몬테카를로 시뮬레이션(Monte-Carlo simulation)에 대해 소개해드릴려고 합니다!
이번 글은 몬테카를로 시뮬레이션 개념과 실무적 측면에서 적용 가능성에 대해 간단히 설명드리려고 합니다.
이름은 무척 거창하지만, 찬찬히 따라오면 충분히 이해하실 수 있으리라 생각이 됩니다.
1. 몬테카를로 시뮬레이션(Monte-Carlo simulation)의 정의
몬테카를로 시뮬레이션은 무작위로 추출된 표본의 값을 반복적으로 계산하고, 이를 큰 수의 법칙에 따라 최종적으로 기대값을 산정하는 이론입니다.
매우 거칠게 요약하자면 특정 가정하에서 시뮬레이션을 매우 많이 돌려서, 그 값들의 기대값으로 미래의 값을 추정하는 것이죠.
예를 들자면 삼성전자의 1년 뒤 주가를 알고 싶은 상황에서,
지금까지의 삼성전자 주가 데이터를 바탕으로 수 천, 수 만번의 주가 변화 시뮬레이션을 돌려서 그것들의 평균으로 1년 뒤 삼성전자의 주가를 추정하는 것입니다.
이는 그래프로 보면 더욱 직관적으로 다가오는데요.

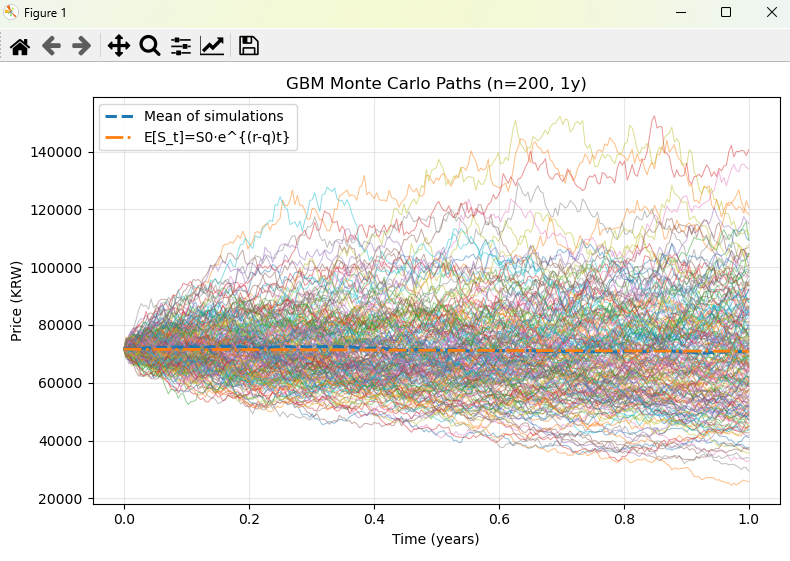
상단 [사진1] 그래프는 현재시점(Time = 0.0)에서 1년 동안의 주가 움직임 시뮬레이션을 200번 생성한 것을 보여주고 있습니다.
(보통 시뮬레이션 한 번 수행에 따른 움직임의 형태를 Path라고 부릅니다.)
각각의 시뮬레이션을 보면 시작점은 100에서 출발했지만, 1년 뒤에 상당히 주가가 많이 상승한 Path들도 있고, 큰 차이가 없는 Path들도 있고, 크게 하락한 Path들도 있다는 것을 알 수 있습니다.
이렇게 만들어진 모든 Path들의 주가를 평균 내어 삼성전자의 향후 1년 뒤의 주가를 추정하는 것입니다.
2. 몬테카를로 시뮬레이션의 특징
이러한 몬테카를로 시뮬레이션의 설명을 보시고선 혹자분들은 어쩌면 '너무 무식한 방법 아니야?' 라고 생각하실 수도 있습니다.
네 맞습니다..!
몬테카를로 시뮬레이션은 설명드린 것처럼 큰 수의 법칙에 의존하는 방법론이기 때문에, 시뮬레이션 횟수가 많으면 많을수록 정확성이 높아질 수 있습니다.
따라서 값을 추정할 때 Path가 많으면 많을수록, 혹은 그 추정값의 계산식이 복잡할수록 계산에 오랜 시간이 소요됩니다.
하지만 이러한 몬테카를로 시뮬레이션의 단점에도 불구하고 몬테카를로 시뮬레이션이 이론적, 실무적으로 유용한 이유 또한 그 무식함, 다르게 말하면 직관성 및 단순성에 기인합니다.
몬테카를로 시뮬레이션은 금융, 수학적으로 매우 복잡한 구조이거나 그 움직임이 매우 드라마틱 하더라도, 그것에 상관없이 수치적인 추정치를 만들어 낼 수 있습니다.
또한 금융공학이나 수학에 조예가 없는 사람이 보더라도, 몬테카를로 시뮬레이션에 의한 가격 추정은 매우 직관적이라 누구나 쉽게 납득 할 수 있다는 점도 큰 장점이라고 할 수 있습니다.
즉 몬테카를로 시뮬레이션은 기존에 존재하는 다른 많은 금융, 수학적 모델을 사용하기 적합하지 않은 경우에 쓸 수 있는 마지막 든든한 보루가 된다고 할 수 있습니다.
3. 몬테카를로 시뮬레이션 모형
몬테카를로 시뮬레이션은 하나의 공식으로 정해져 있지 않습니다.
기대값을 추정한다는 틀 아래에서, 추정하고자 하는 값이 무엇인지에 따라 기하브라운(GBM, Geometric Brownian Motion), VAR, Hull-White 등 다양한 모형을 사용하고 있습니다.
하지만 이번 글에서는 그중에서도 대표적으로 가장 많이 사용되는 GBM 모형을 통해 주가를 추정하는 것을 설명드리도록 하겠습니다.
금융모델에서 사용되는 리스크중립 확률측도의 GBM의 공식은 다음과 같습니다.
\( S_T = S_0 \cdot \exp \Big( (r - q - \tfrac{1}{2}\sigma^2)T + \sigma \sqrt{T} Z \Big), \quad Z \sim \mathcal{N}(0,1) \)
순간 복잡한 공식에 당황하셨을 수도 있다고 생각합니다.
하지만 오늘은 GBM이 메인이 아니니, 그냥 GBM의 모형이 이렇구나라고만 생각해주시고 받아들여주시면 되겠습니다.
각각의 변수는 다음과 같은 의미를 가집니다.
\( S_T\) : 추정하고 싶은 값
\( S_0\) : 초기시점의 값
\( r\) : 무위험이자율(Risk Free)
\( q\) : 배당수익률
\( sigma\) : 변동성
\( T\) : 추정치까지 남은 기간(혹은 잔존만기)
\( Z\) : 가정하고 있는 확률분포
\( Z \sim \mathcal{N}(0,1) \) : 표준정규분포
이 GBM의 공식을 통해 도출되는 것이 각 Path 속 한 개의 Step의 값입니다.
Step은 값을 추정하는 가장 작은 단위라고 생각하시면 되고, 미래 주가를 추정하는 경우에는 각 영업일이 Step이 될 것입니다.
이렇듯 GBM 공식을 통해 미래의 주가를 추정하는 방법은, 오늘의 주가를 바탕으로 다음 영업일의 주가를 추정하고, 그 추정한 주가를 바탕으로 그 다음 영업일의 주가를 추정하는 것을 반복하는 것입니다.
만약 앞으로 1년 후의 주가를 추정한다면 하나의 Path에는 1년 후까지의 모든 영업일마다 상단의 GBM 공식을 적용하는 것입니다.
따라서 1년동안의 영업일을 약 250회라고 가정하면, 하나의 Path를 그리는데 필요한 계산은 250번입니다.
그리고 이 Path를 [그림1]처럼 200개를 만들려고 한다면 총 필요한 계산수는 250*200 = 50,000입니다.
물론 현업에서 실제로 적용되는건 적어도 수 천회 이상부터입니다.
그러니 아무리 컴퓨터로 계산을 돌린다고 하더라도, 계산 시간이 소요될 수밖에 없는 것이지요.
4. (응용) Python에서 GBM 공식을 활용해 미래주가 추정
그러면 실제로 아주 간단하게 파이썬에서 GBM 식을 통해 미래 주가를 추정해보겠습니다.
물론 하단에 설정된 파라미터 값들은 제가 임의적으로 설정한 것이므로 실제와 다릅니다.
각 코드에 대한 설명은 간단히 주석으로 남기었으니, 이해하시는데 도움이 될 것 같습니다!
또한 해당 코드를 보면 앞서 설명한 수식을 코드로 구현한 것을 알 수 있을 것 같습니다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
from datetime import datetime, timedelta
# 1) 파라미터 설정
S0 = 71600 # 현재 주가 (예: 2025-08-14 기준)
r = 0.01 # 무위험수익률
q = 0.02 # 배당수익률
sigma = 0.30 # 연간 변동성
T = 1.0 # 추정기간(년)
n_sims = 100_000 # 만기 ST 분포용 샘플 수
n_paths = 200 # 경로 그래프에 그릴 경로 수
n_steps = 252 # 1년 거래일 가정
seed = 12345 # 랜담시드 설정
rng = np.random.default_rng(seed)
# 2) GBM 모형 사용
Z = rng.standard_normal(n_sims)
ST = S0 * np.exp((r - q - 0.5 * sigma**2) * T + sigma * np.sqrt(T) * Z) # GBM 모형 사용
mean_ST = ST.mean() # 평균값
median_ST = np.median(ST) # 중앙값
p05, p25, p75, p95 = np.percentile(ST, [5, 25, 75, 95]) # Q1~Q4
rn_expectation = S0 * np.exp((r - q) * T) # 리스크중립측도 하에서 미래 주가의 기댓값
# 3) 경로 시뮬레이션 (다중 스텝)
dt = T / n_steps
t = np.linspace(0.0, T, n_steps + 1)
Z_paths = rng.standard_normal((n_paths, n_steps)) # 표준정규 난수
increments = (r - q - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z_paths # GBM 이산화
log_paths = np.cumsum(increments, axis=1)
log_paths = np.hstack([np.zeros((n_paths, 1)), log_paths])
S_paths = S0 * np.exp(log_paths)
# 4) 값 출력
print({
"inputs": {"S0": S0, "r": r, "q": q, "sigma": sigma, "T": T, "n_sims": n_sims},
"MC_mean_ST": round(float(mean_ST), 2),
"MC_median_ST": round(float(median_ST), 2),
"MC_5%": round(float(p05), 2),
"MC_25%": round(float(p25), 2),
"MC_75%": round(float(p75), 2),
"MC_95%": round(float(p95), 2),
"RiskNeutral_E[ST]": round(float(rn_expectation), 2)
})
# 5) 경로 그래프
plt.figure(figsize=(8, 5))
for i in range(n_paths):
plt.plot(t, S_paths[i], linewidth=0.7, alpha=0.5)
plt.plot(t, S_paths.mean(axis=0), linewidth=2.2, linestyle="--", label="Mean of simulations")
plt.plot(t, S0 * np.exp((r - q) * t), linewidth=2.0, linestyle="-.", label="E[S_t]=S0·e^{(r-q)t}")
plt.title("GBM Monte Carlo Paths (n=200, 1y)")
plt.xlabel("Time (years)")
plt.ylabel("Price (KRW)")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
이러한 파이썬 코드로 몬테카를로 시뮬레이션의 Path 모습은 [그림2]와 같고, 1년 후의 주가는 71,001원이네요..!
1년 후에 실제 주가와 얼마나 큰 차이가 날지도 궁금해집니다.
이로써 금융 속 파생상품과 주가 추정 등에 자주 쓰이는 몬테카를로 시뮬레이션과 몬테카를로 시뮬레이션 모형에 주로 사용되는
GBM 모델에 대해서도 간단히 설명 드렸습니다.
차후에 기회가 된다면 파이썬뿐만 아니라 VBA로도 설명 드리거나, GBM 공식을 도출하는 것도 작성하겠습니다.
긴 글 읽어주셔서 감사합니다. 조금이라도 도움이 되셨길 바랍니다!
''금'융' 카테고리의 다른 글
| [금융] 신주인수권부사채(BW, Bond with Warrant) (0) | 2025.10.19 |
|---|---|
| [금융] 교환사채(EB, Exchangeable Bond)의 개념과 발행 요소 (2) | 2025.07.20 |
| [금융] 전환사채(CB, Convertible Bond)의 발행 요소 (2) | 2025.06.08 |
| [금융] 메자닌 상품(Mezzanine) 의 정의와 종류 (1) | 2025.03.16 |
| [금융공학] 미래가치(FV)를 통한 현재가치(PV) 계산 (0) | 2025.02.02 |



